Class 9 Maths Chapter 10 Previous Year Questions - Heron`s Formula
Very Short Answer Type Questions
Q1. Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm.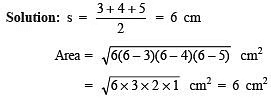
Q2. If the area of an equilateral is √3/4 cm2 then find the side of the triangle.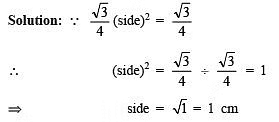
Short Answers Type Questions
Q1. The length of a rectangular plot of land is twice its breadth. If the perimeter of the plot be 180 metres, then find its area.
Sol:
Let the breadth of the plot be ‘x’ metres.
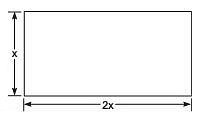 ∴ Its length = 2x metresSince perimeter of a rectangular plot = 2[Length + Breadth]∴ Perimeter of the given plot = 2[x + 2x]= 2[3x]= 6x metres
∴ Its length = 2x metresSince perimeter of a rectangular plot = 2[Length + Breadth]∴ Perimeter of the given plot = 2[x + 2x]= 2[3x]= 6x metres
⇒ 6x = 180
⇒ x= 180/6= 30 metres
⇒ 2x = 2 x 30 = 60 metres.
∴ Length of the plot = 60 metres and Breadth of the plot = 30 meters.
∴ Area of the plot = Length x Breadth = 60 x 30 m2 = 1800 m2
Q2. The length of the sides containing the right angle in a right triangle differ by 7 cm. The area of the triangle is 60 cm2. Find the length of the hypotenuse.
Sol:
Let the sides containing the right angle be ‘x’ cm and (x – 7) cm.
i.e. Base = x cm and height = (x – 7) cm
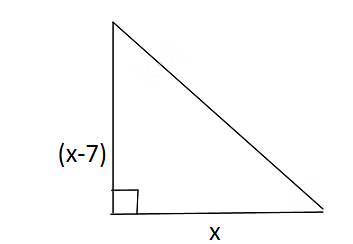
∴ Area = (1/2) x base x height=(1/2) x x x (x – 7) cm2
Now (1/2) x (x – 7) = 60
⇒ x(x – 7) = 120
⇒ x2 – 7x – 120 = 0
⇒ x2 – 15x + 8x – 120 = 0
⇒ x(x – 15) + 8(x – 15) = 0
⇒ (x + 8)(x – 15) = 0
⇒ x = – 8 or x = 15
Rejecting x = –8, we have x – 15 = 0
⇒ x = 15 cm x – 7 = 15 – 7 = 8 cm
Now, Hypotenuse 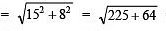 = √289 = 17cmThus, the required length of the hypotenuse is 17 cm.
= √289 = 17cmThus, the required length of the hypotenuse is 17 cm.
Q3. Find the area of a quadrilateral ABCD in which AB = 8 cm, BC = 6 cm, CD = 8 cm, DA = 10 cm and AC = 10 cm.
Sol:
In ΔABC, ∠B = 90°
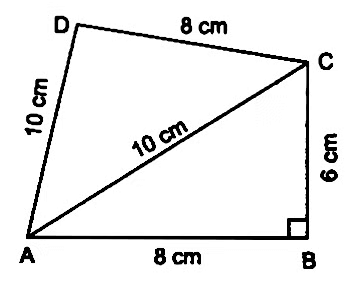
∴ area of right (rt ΔABC) = (1/2) x 8 x 6 cm2 = 24 cm2
In ΔACD,
a = AC = 10 cm b = AD = 10 cm c = CD = 8 cm
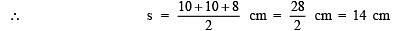
∴Area of ΔACD
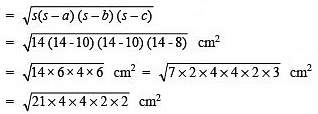
= 2 x 4√21 = 8√21 cm2
= 8 x 4,58 cm2 = 36.64 cm2
Now, area of quadrilateral ABCD = ar (ΔABC) + ar (ΔACD)
= 24 cm2 + 8√21 cm2
= 24 cm2 + 36.64 cm2
= 60.64 cm2
Q4. How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square of diagonal 44 cm.
Sol:
∵ The diagonals of a square bisect each other at right angles
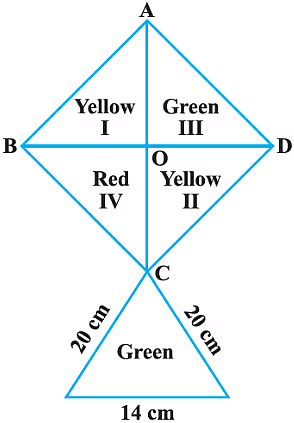
∴ OB = OD = OA = OC = (44/2) = 22 cm
Now, ar rt (Δ –I) = (1/2)× OB × OA
= (1/2) × 22 × 22 cm2 = 242 cm2
Similarly ar rt (Δ –II) = arrt(Δ–III) = ar rt (Δ –IV) = 242 cm2
∵ Sides of ΔCEF are 20 cm, 20 cm and 14 cm
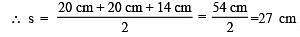
⇒ Area of ΔCEF
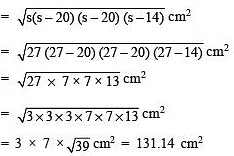
Now, area of yellow paper = ar (Δ – I) + ar (Δ – II)
= 242 cm2 + 242 cm2 = 484 cm2
Area of red paper = ar (Δ – IV) = 242 cm2
Area of green paper = ar (Δ – III) + ar ΔCEF
= 242 cm2 + 131.14 cm2
= 373.14 cm2
Long Answer Type Questions
Q1: The perimeter of a triangular field is 144 m and its sides are in the ratio 3:4:5. Find the length of the perpendicular from the opposite vertex to the side whose length is 60 m.
Sol:
Let the sides of the triangle be 3x, 4x and 5x
∴ The perimeter of the triangular field = 144 m
⇒ 3x + 4x + 5x = 144
⇒ 12x = 144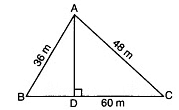
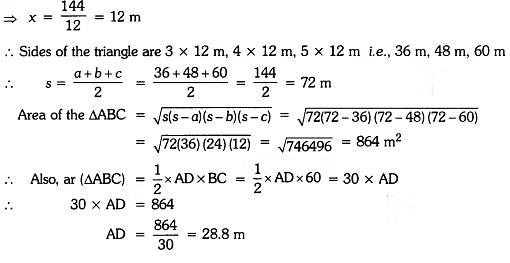
Q2: Find the area of the triangle whose perimeter is 180 cm and two of its sides are of lengths 80 cm and 18 cm. Also, calculate the altitude of the triangle corresponding to the shortest side.
Sol:
Perimeter of given triangle = 180 cm
Two sides are 18 cm and 80 cm
∴ Third side = 180 – 18 – 80 = 82 cm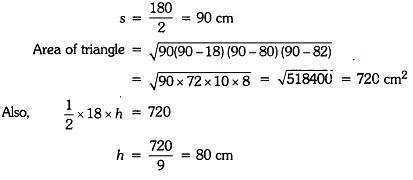
Hence, area of triangle is 720 cm2 and altitude of the triangle corresponding to the shortest side is 80 cm.
Q3: The sides of a triangular park are 8 m, 10 m and 6 m respectively. A small circular area of diameter 2 m is to be left out and the remaining area is to be used for growing roses. How much area is used for growing roses ? (use n = 3.14)
Sol:
The sides of the triangular park are 8 m, 10 m and 6 m.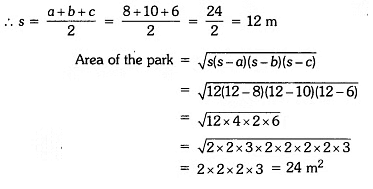
Radius of the circle = 2/2 = 1 m
Area of the circle = πr2 = 3.14 × 1 × 1 = 3.14 m2
∴ Area to be used for growing roses = Area of the park – area of the circle
= 24 – 3.14 = 20.86 m2
|
40 videos|560 docs|57 tests
|
FAQs on Class 9 Maths Chapter 10 Previous Year Questions - Heron`s Formula
| 1. What is Heron's Formula and how is it derived? |  |
| 2. How do you apply Heron's Formula to find the area of a triangle with sides 7, 8, and 9? |  |
| 3. What are the limitations of using Heron's Formula? |  |
| 4. Can Heron's Formula be used for obtuse and acute triangles? |  |
| 5. What is the relationship between Heron's Formula and the triangle inequality theorem? |  |





















